If you need to find some similar objects in vector space, provided e.g. by embeddings or matching NN, you can choose among a variety of libraries: Annoy, FAISS or NMSLib. All of them will give you a fast approximate neighbors search within almost any space.
But what if you need to introduce some constraints in your search? For example, you want search only for products in some category or select the most similar customer of a particular brand. I did not find any simple solutions for this. There are several discussions like this, but they only suggest to iterate over top search results and apply conditions consequently after the search.
Let’s see if we could somehow modify any of ANN algorithms to be able to apply constrains during the search itself.
Annoy builds tree index over random projections. Tree index implies that we will meet same problem that appears in relational databases: if field indexes were built independently, then it is possible to use only one of them at a time. Since nobody solved this problem before, it seems that there is no easy approach.
There is another algorithm which shows top results on the benchmark. It is called HNSW which stands for Hierarchical Navigable Small World.
The original paper is well written and very easy to read, so I will only give the main idea here.
We need to build a navigation graph among all indexed points so that the greedy search on this graph will lead us to the nearest point.
This graph is constructed by sequentially adding points that are connected by a fixed number of edges to previously added points.
In the resulting graph, the number of edges at each point does not exceed a given threshold
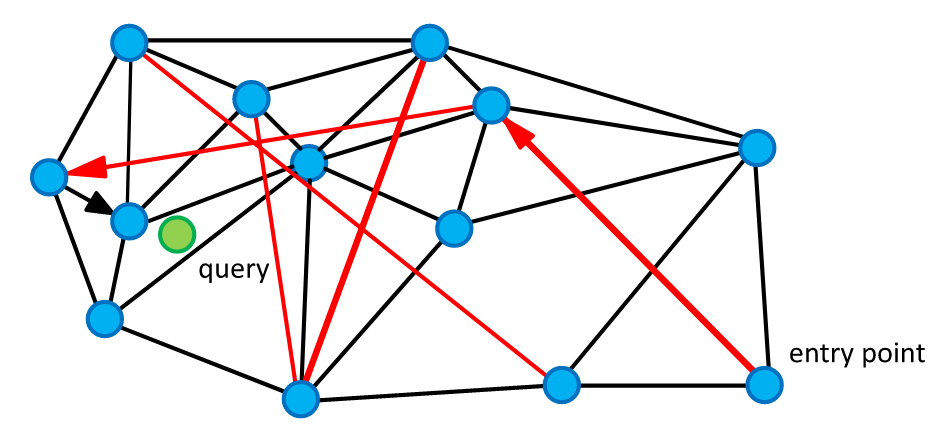
How can we modify it?
What if we simply apply the filter criteria to the nodes of this graph and use in the greedy search only those that meet these criteria? It turns out that even with this naive modification algorithm can cover some use cases.
One such case is if your criteria do not correlate with vector semantics. For example, you use a vector search for clothing names and want to filter out some sizes. In this case, the nodes will be uniformly filtered out from the entire cluster structure. Therefore, the theoretical conclusions obtained in the Percolation theory become applicable:
Percolation is related to the robustness of the graph (called also network). Given a random graph of
nodes and an average degree . Next we remove randomly a fraction of nodes and leave only a fraction . There exists a critical percolation threshold below which the network becomes fragmented while above a giant connected component exists.
This statement also confirmed by experiments:
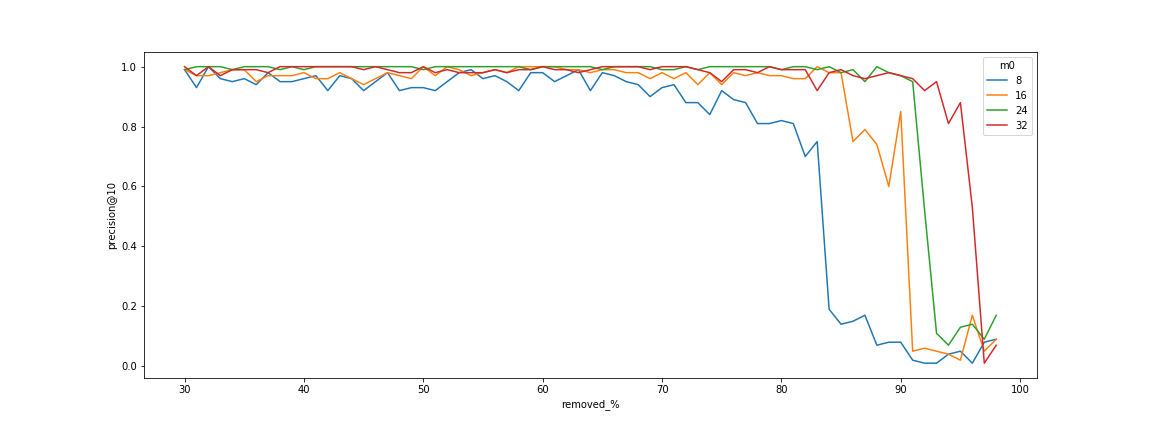
Dependency of connectivity to the number of edges
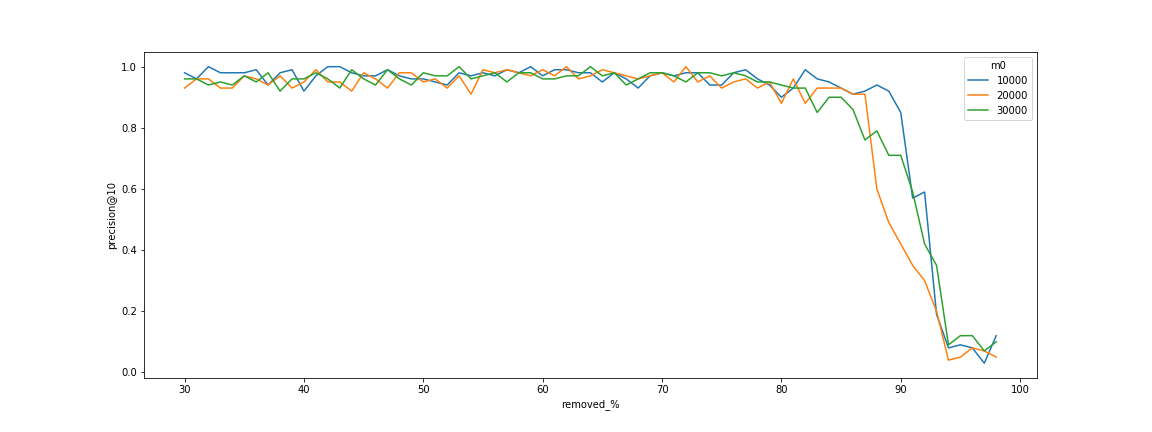
Dependency of connectivity to the number of point (no dependency).
There is a clear threshold when the search begins to fail.
This threshold is due to the decomposition of the graph into small connected components.
The graphs also show that this threshold can be shifted by increasing the
Let’s consider some other filtering conditions we might want to apply in the search:
- Categorical filtering
- Select only points in a specific category
- Select points which belong to a specific subset of categories
- Select points with a specific set of labels
- Numerical range
- Selection within some geographical region
In the first case, we can guarantee that the HNSW graph will be connected simply by creating additional edges inside each category separately, using the same graph construction algorithm, and then combining them into the original graph. In this case, the total number of edges will increase by no more than 2 times, regardless of the number of categories.
Second case is a little harder. A connection may be lost between two categories if they lie in different clusters.
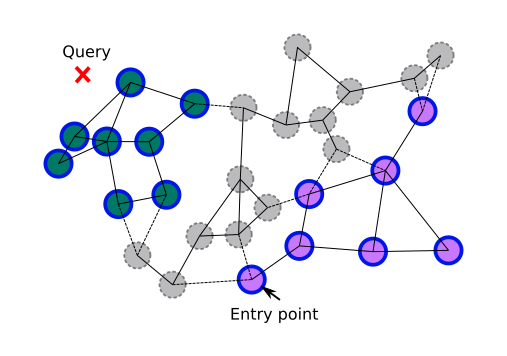
The idea here is to build same navigation graph but not between nodes, but between categories. Distance between two categories might be defined as distance between category entry points (or, for precision, as the average distance between a random sample). Now we can estimate expected graph connectivity by number of excluded categories, not nodes. It still does not guarantee that two random categories will be connected, but allows us to switch to multiple searches in each category if connectivity threshold passed. In some cases, multiple searches can be even faster if you take advantage of parallel processing.
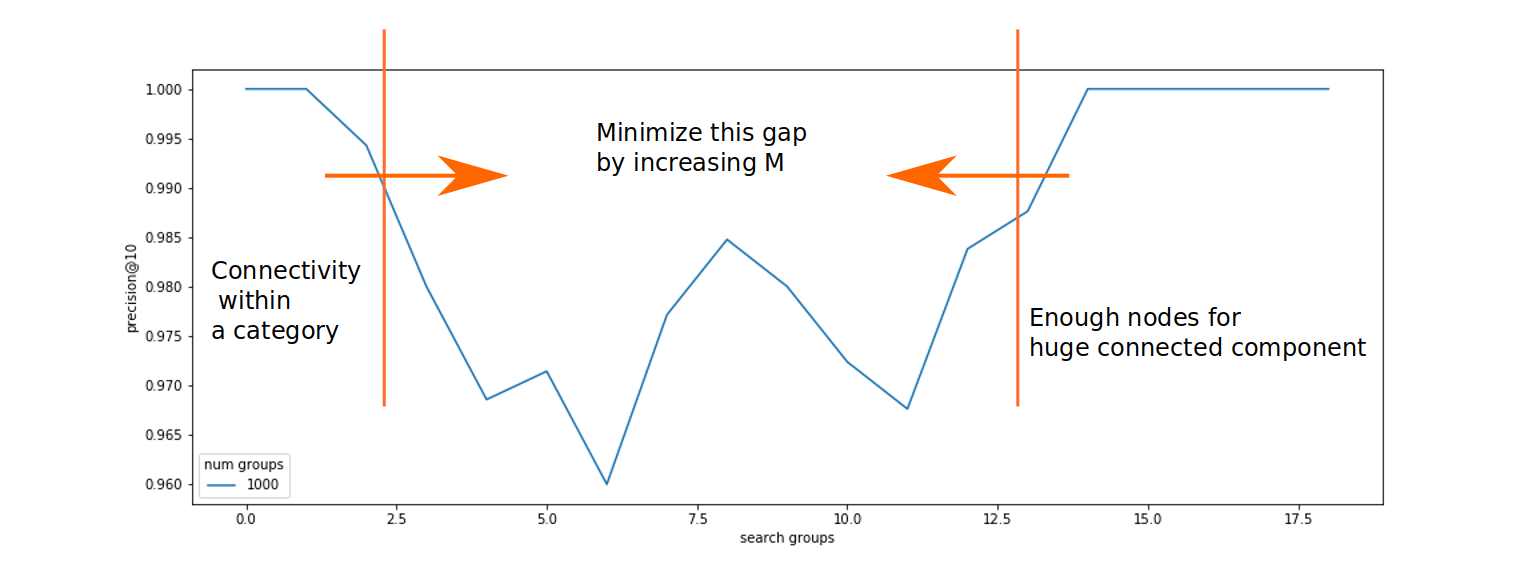
Dependency of connectivity to the random categories included in search
Third case might be resolved in a same way it is resolved in classical databases. Depending on labeled subsets size ration we can go for one of the following scenarios:
- if at least one subset is small: perform search over the label containing smallest subset and then filter points consequently.
- if large subsets give large intersection: perform regular search with constraints expecting that intersection size fits connectivity threshold.
- if large subsets give small intersection: perform linear search over intersection expecting that it is small enough to fit a time frame.
Numerical range case can be reduces to the previous one if we split numerical range into a buckets containing equal amount of points. Next we also connect neighboring buckets to achieve graph connectivity. We still need to filter some results which presence in border buckets but do not fulfill actual constraints, but their amount might be regulated by the size of buckets.
Geographical case is a lot like a numerical one. Usual geographical search involves geohash, which matches any geo-point to a fixes length identifier.
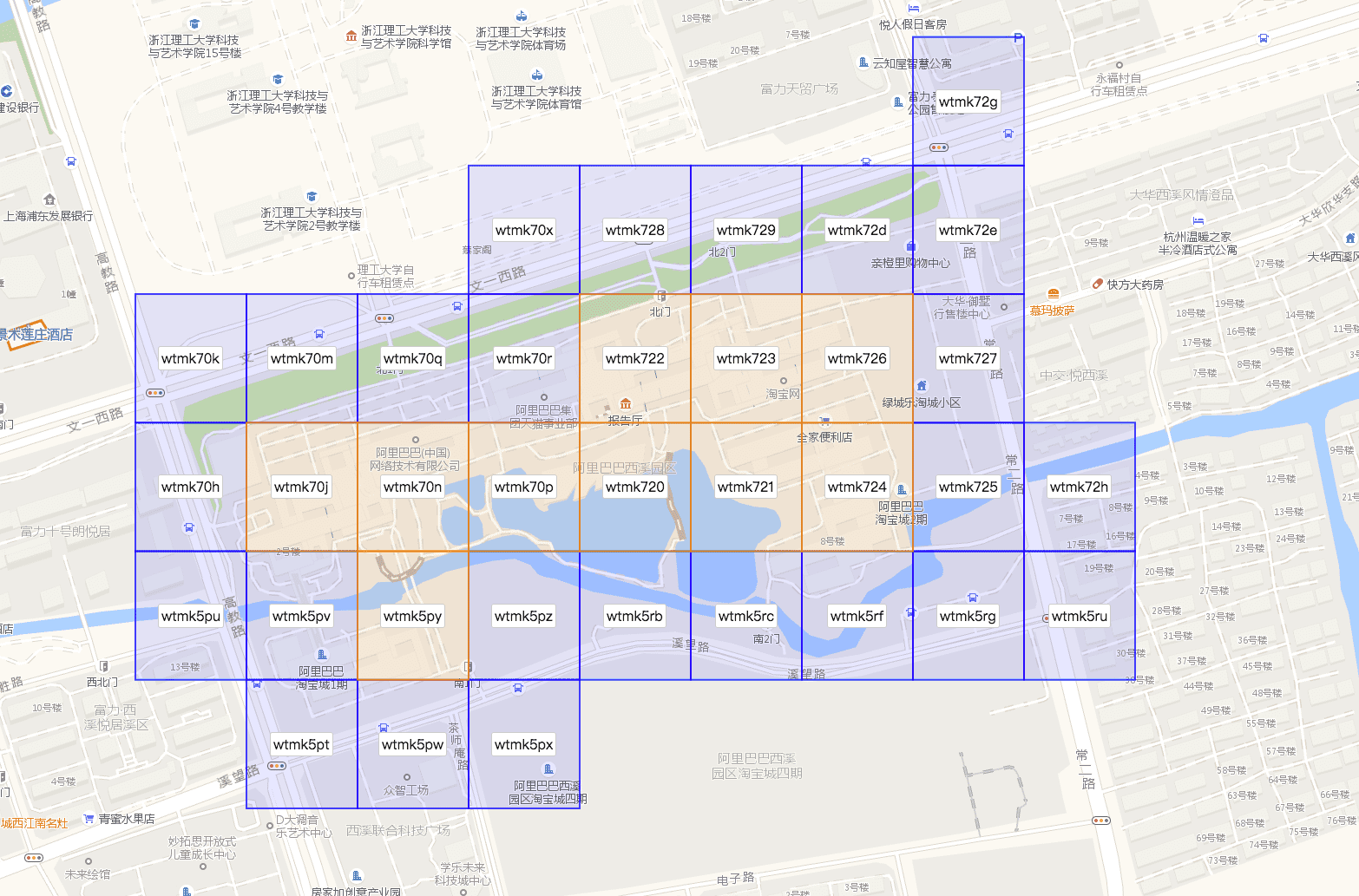
We can use this identifiers as categories and additionally make connections between neighboring geohashes. It will ensure that any selected geographical region will also contain connected HNSW graph.
Conclusion
It is possible to enchant HNSW algorithm so that it will support filtering points in a first search phase. Filtering can be carried out on the basis of belonging to categories, which in turn is generalized to such popular cases as numerical ranges and geo.
Experiments were carried by modification python implementation of the algorithm, but real production systems require much faster version, like NMSLib.

