Day 3

Sparse Vectors and Inverted Indexes

Create and index sparse vector representations for keywords-based search and recommendations.

What You’ll Learn

Understanding sparse vector representations
Using sparse vectors in Qdrant

Sparse Vector Representations

Sparse vectors are high dimensional vectors, filled up with zeroes except for a few dimensions. Each dimension of a sparse vector refers to a certain object, and its value – a role of this object in this sparse representation.

Let’s consider a movie recommendation system:

Each sparse vector could describe a particular user’s opinion.
Each dimension could describe a certain movie M_X, and its value – user’s rating of this movie.

         M1  M2  M3  M4  M5  M6  M7  M8  M9  M10
User_1: [ 0,  0,  0,  0,  0,  0,  1,  5,  0,  0 ]
User_2: [ 0,  0,  0,  0,  4,  0,  0,  2,  0,  0 ]

Comparing Sparse Representations

Comparing two sparse representations, you’d be usually interested in how much they agree on the same features/objects (e.g., the same movie rating).

The dot product distance metric, introduced in the day 1 (Vector Search Fundamentals/Distance Metrics), is a perfect fit for measuring the similarity between sparse representations. It multiplies corresponding dimensions and summes the results.

similarity(User_1, User_2) = 0*0 + ... + 0*4 + ... + 1*0 + 5*2 + ... 0*0 = 10

You can notice that only objects/features that play a role in both vectors (non-zero dimensions in both) affect the final score.

Representations as Index-Value Pairs

Storing thousands of zeros contributing no information is wasteful.
Instead, a sparse vector can be stored compactly as (index, value) pairs of its non-zero entries.

Using the movie example:

[0, 0, 0, 0, 0, 0, 1.0, 2.0, 0, 0]
 0  1  2  3  4  5   6    7   8  9

→ [(6, 1.0), (7, 2.0)]

This representation is space-efficient and preserves exactly the information that impacts sparse vectors similarity.

Organizing Sparse Vectors: Inverted Index

Searching for similar sparse vectors boils down to finding the vectors that share non‑zero dimensions with the query and multiplying corresponding values.

Scanning every vector to check for matching non-zero dimensions is too slow at scale.

Simple idea: keep a map from dimension index to vectors that have these dimensions non-zero (with the corresponding weights). At query time:

For each query non-zero dimension, check that map entry to collect matching vectors.
Score only those candidates using the dot product over the overlapping non-zero indices.

Example

Let’s grasp it on a simple example:

We have 3 documents - 3 sparse vector representations:

id_1: [(6, 1.0), (12, 2.0)]
id_2: [(1, 0.2), (7, 1.0)]
id_3: [(6, 0.3), (7, 2.0), (12, -0.5)]

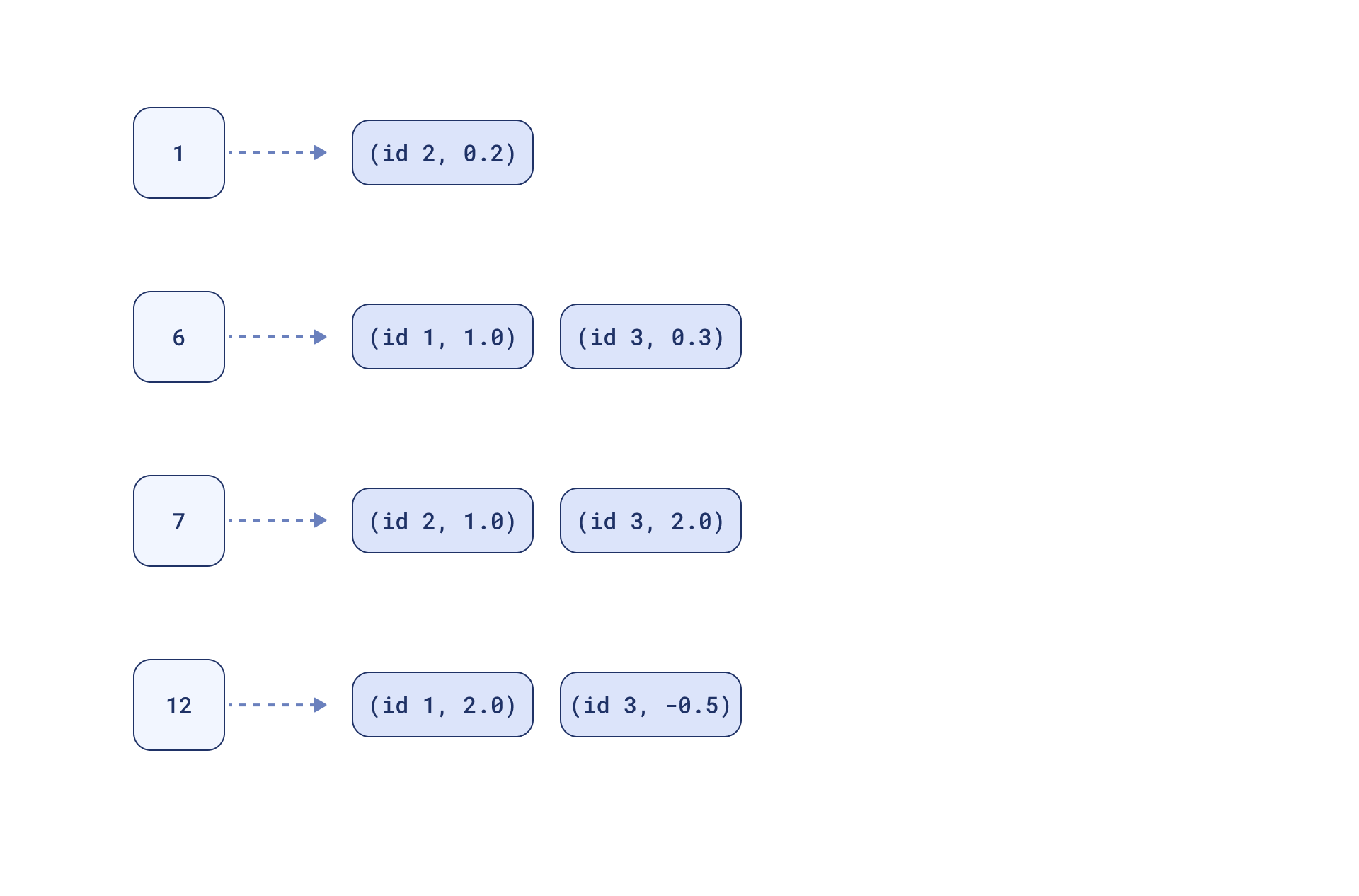
The proposed map could look like this: Inverted index: map from index to vectors with weights

Now, if we have a query:

[(6, 1.0), (7, 2.0)]

Search will consist of looking up 6 and 7 in the map & computing scores on the overlaps:

id_1: (6: 1.0*1.0)                 = 1.0
id_2: (7: 2.0*1.0)                 = 2.0
id_3: (6: 1.0*0.3) + (7: 2.0*2.0)  = 0.3 + 4.0 = 4.3

This simple map is the essence of an inverted index, a data structure organizing sparse vector elements in a retrieval system. It inverts the representation by mapping each non‑zero dimension to the vectors where it appears.

Inverted index makes sure sparse search stays exact and fast even at large scale.

Sparse Vectors in Qdrant

Follow along in Colab:

Sparse vectors in Qdrant collections are configured using sparse_vectors_config.

Unlike in dense vector configuration, we don’t need to define size or distance metric for sparse vectors:

Size varies based on the number of non-zero elements in the sparse vector.
- The maximum number of non-zero elements (i.e., the sparse vector’s size) is limited by the uint32 type, meaning 4,294,967,296 non-zero elements.
Distance metric for comparing sparse vectors is always the Dot product.

Sparse vectors are not the default in Qdrant (unlike dense vectors). That’s why, to configure collection with sparse vectors, you’ll always need to give them a name.

Named vectors additionally allow us to use multiple vectors for the same point, for example, one dense and one sparse. We’ll cover more about this in the upcoming videos on Hybrid Search.

Create a Collection with Sparse Vectors

# Create collection with a named sparse vector
client.create_collection(
    collection_name=<COLLECTION_NAME>,
    sparse_vectors_config={
        <SPARSE_VECTOR_NAME>: models.SparseVectorParams()
    },
)

(Optional) Tune the Inverted Index

Defaults are chosen to work well; tune only if you understand the trade‑offs!

Parameters:

full_scan_threshold (int) – up to this number (not including), the inverted index won’t be used during comparison (but is still built).
on_disk (bool) – store the inverted index on disk (True) or in RAM (False, default).
datatype – precision of values stored inside the index: uint8 | float16 | float32 (default).
- The original values are still stored on disk regardless of the datatype value.

client.create_collection(
    collection_name=<COLLECTION_NAME>,
    sparse_vectors_config={
        <SPARSE_VECTOR_NAME>: models.SparseVectorParams(
            index=models.SparseIndexParams(
                full_scan_threshold=0,          # compare directly below this size (index still built)
                on_disk=False,                  # keep index in RAM (default False)
                datatype=models.VectorStorageDatatype("float32")  # precision inside the index
            )
        )
    },
)

Store Sparse Vectors in Qdrant

Sparse vectors in Qdrant are represented by:

indices – the indices of non-zero dimensions (stored as uint32, so they can range from 0 to 4,294,967,295).
- indices must be unique within a vector.
values – the values of these non-zero dimensions (stored as a float).
- len(indices) == len(values).

client.upsert(
    collection_name=<COLLECTION_NAME>,
    points=[
        models.PointStruct(
            id=1,
            vector={<SPARSE_VECTOR_NAME>: models.SparseVector(
                indices=[1,2,3], 
                values=[0.2,-0.2,0.2]
            )}
        ),
        ...
    ],
)

Don’t confuse a vector’s indices with the inverted index.

indices describe which dimensions are non‑zero for the vector.
The inverted index is a data structure that maps each dimension to all vectors where it is non‑zero.

Run Similarity Search on Sparse Vectors

Specify the named vector to search with using="sparse_vector".

client.query_points(
    collection_name="sparse_vectors_collection",
    using=<SPARSE_VECTOR_NAME>,
    query=models.SparseVector(indices=[1,3], values=[1,1]),
    ...
)

The similarity score for sparse vectors is calculated by comparing only the matching indices shared between the query and the points.

Key Takeaways

Choose sparse vectors when most features are absent (zero) and you need exact, feature-aligned matching.
They’re storage-efficient and work well alongside dense vectors in future Hybrid Search setups.
Similarity = Dot product. Sparse vector similarity in Qdrant is always measured by the dot product.
Sparse vectors are organized in inverted index (separate data structure from HNSW, which is used for dense vectors).
Search on sparse vectors in Qdrant is exact, as opposed to approximate dense vector search.

What’s Next

In the next video, we’ll build keyword-based retrieval with sparse vectors in Qdrant.
We’ll use BM25 and touch on sparse neural retrieval, keyword-based retrieval with semantic understanding. This will set you up for hybrid search pipelines covered in the second half of this day’s material.

Continue to Next Step