MUVERA: Making Multivectors More Performant
Kacper Łukawski
·September 05, 2025

What are MUVERA Embeddings?
Multi-vector representations are superior to single-vector embeddings in many benchmarks. It might be tempting to use them right away, but there is a catch: they are slower to search. Traditional vector search structures like HNSW are optimized for retrieving the nearest neighbors of a single query vector using simple metrics such as cosine similarity. These indexes are not suitable for multi-vector retrieval strategies, such as MaxSim, where a query and document are each represented by multiple vectors and the final score is computed as the maximum similarity over all cross-pairings. MaxSim is inherently asymmetric and non-metric, so HNSW could potentially help us find the closest document token to a given query token, but that does not mean the whole document is the best hit for the query.
MUVERA embeddings, introduced by Google Research, aim to solve this problem. The idea is to create a single vector that approximates the multi-vector representation. This single vector can be used for fast initial retrieval using traditional vector search methods, and then the multi-vector representation can be used for reranking the top results. This approach combines the speed of single-vector search with the accuracy of multi-vector retrieval. Reranking with multi-vector representations is much faster when applied to a small set of candidates rather than the entire dataset.
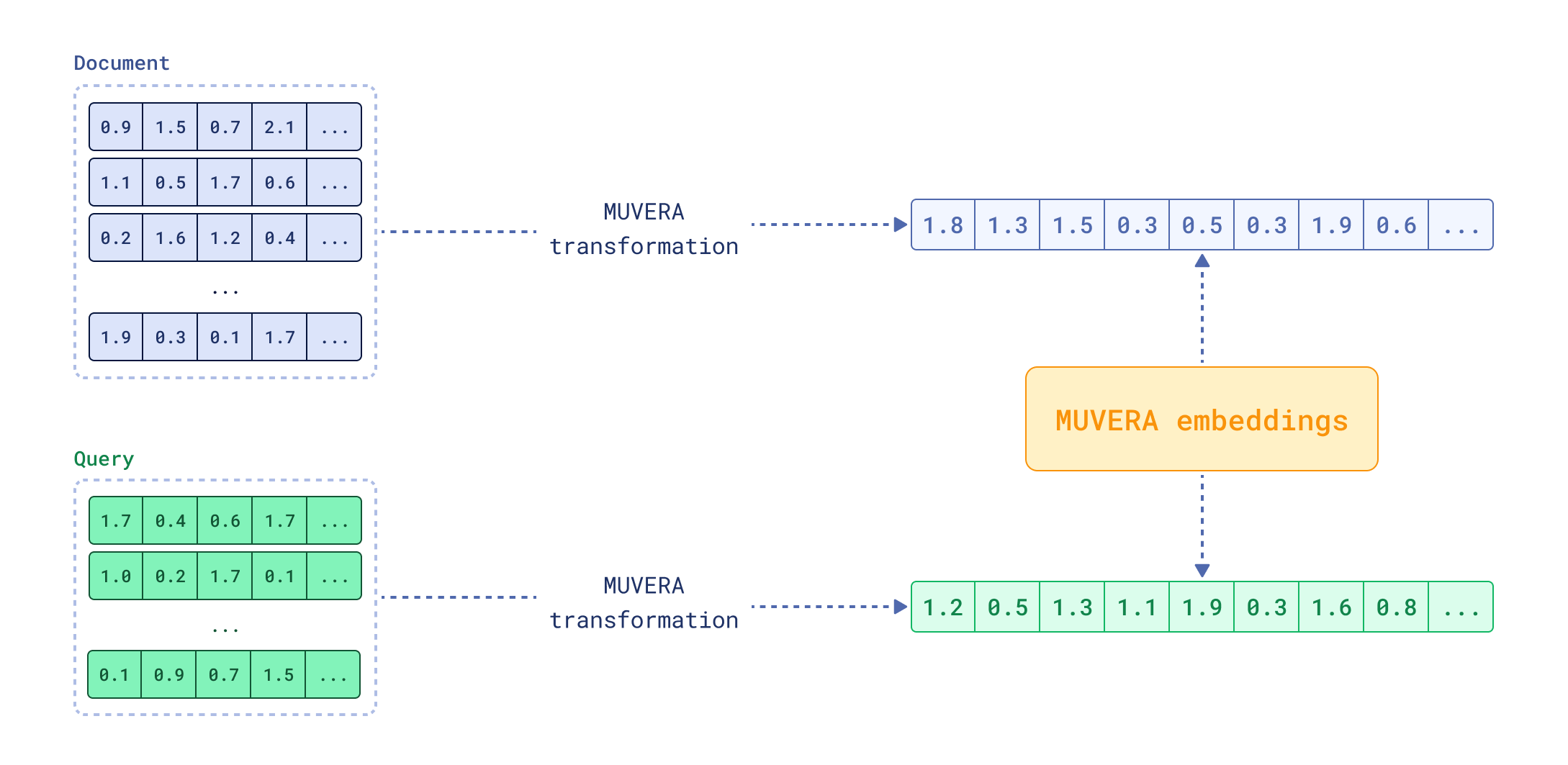
FastEmbed 0.7.2 introduces support for MUVERA embeddings, and this article explains the concept in detail.
How MUVERA Embeddings are created
MUVERA (Multi-Vector Retrieval Algorithm) transforms variable-length sequences of vectors into fixed-dimensional representations. Since the number of vectors in the input varies between documents and queries, and might be even different between different documents, we need a universal way to represent them in a fixed-size format. Clustering the vector space of the tokens and projecting the individual multi-vector representations to a lower-dimensional space using the created clustering helps achieve this. The authors of the MUVERA paper suggest using the Locality-Sensitive Hashing (LSH) technique called SimHash.
Glossary of parameters
There are a few parameters that control the MUVERA embedding creation process, so in order to avoid confusion, here is a quick definition of them:
dim: Dimensionality of a single token vector in the original multi-vector representation, depends on the model usedk_sim: Number of random hyperplanes used in SimHash, which determines the number of clusters as2^k_simdim_proj: Dimensionality of the projected vectors after random projectionr_reps: Number of independent repetitions of the SimHash projection and random projection process
SimHash projection for clustering
SimHash is one of the LSH techniques that uses random hyperplanes to hash input vectors into binary codes. In the first
step, this method chooses k_sim random hyperplanes (normal vectors) from a standard normal distribution. These
hyperplanes divide the vector space into 2^k_sim regions, because each vector can be on either side of each
hyperplane. Here is how such a space division could look like for k_sim=3:
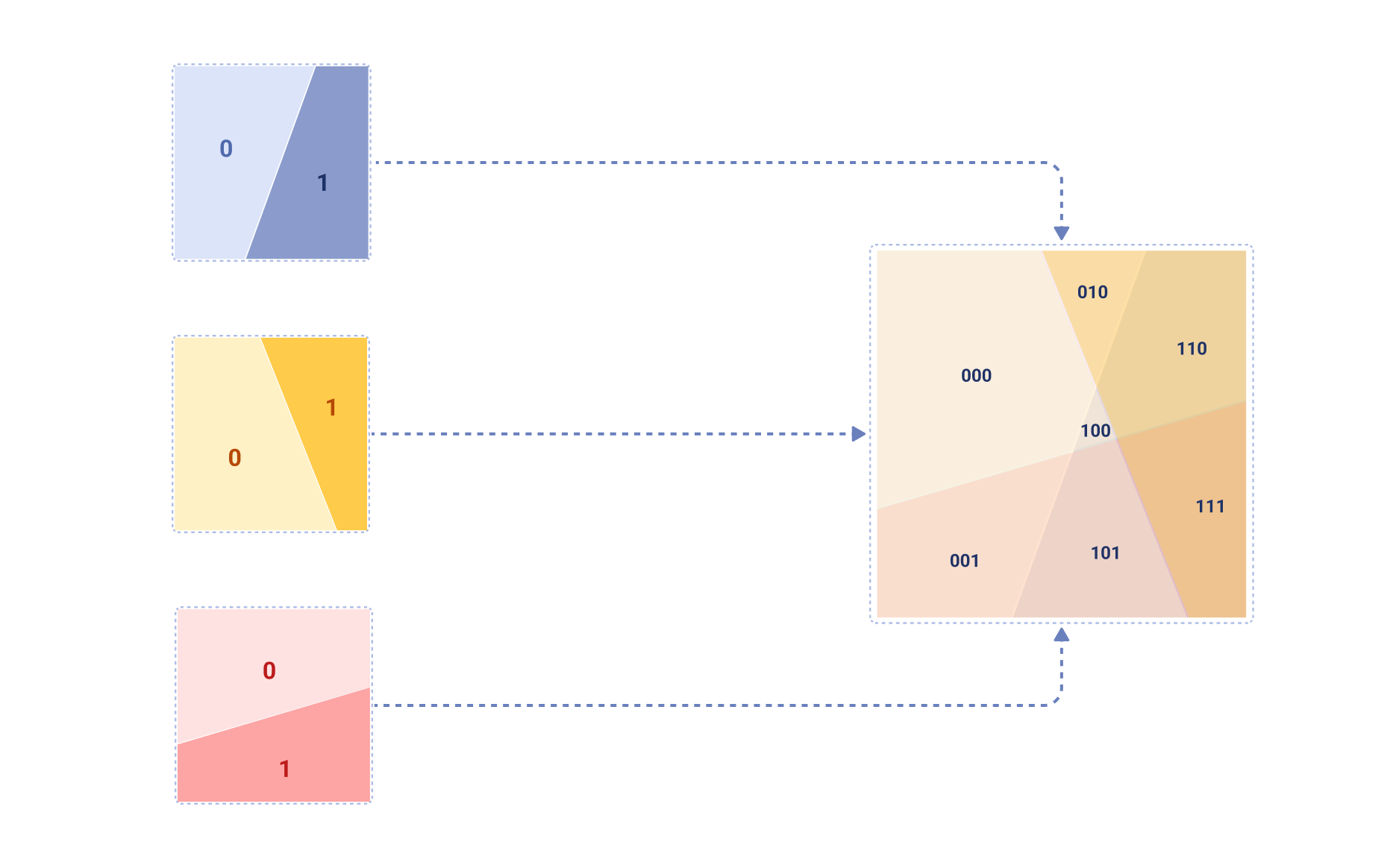
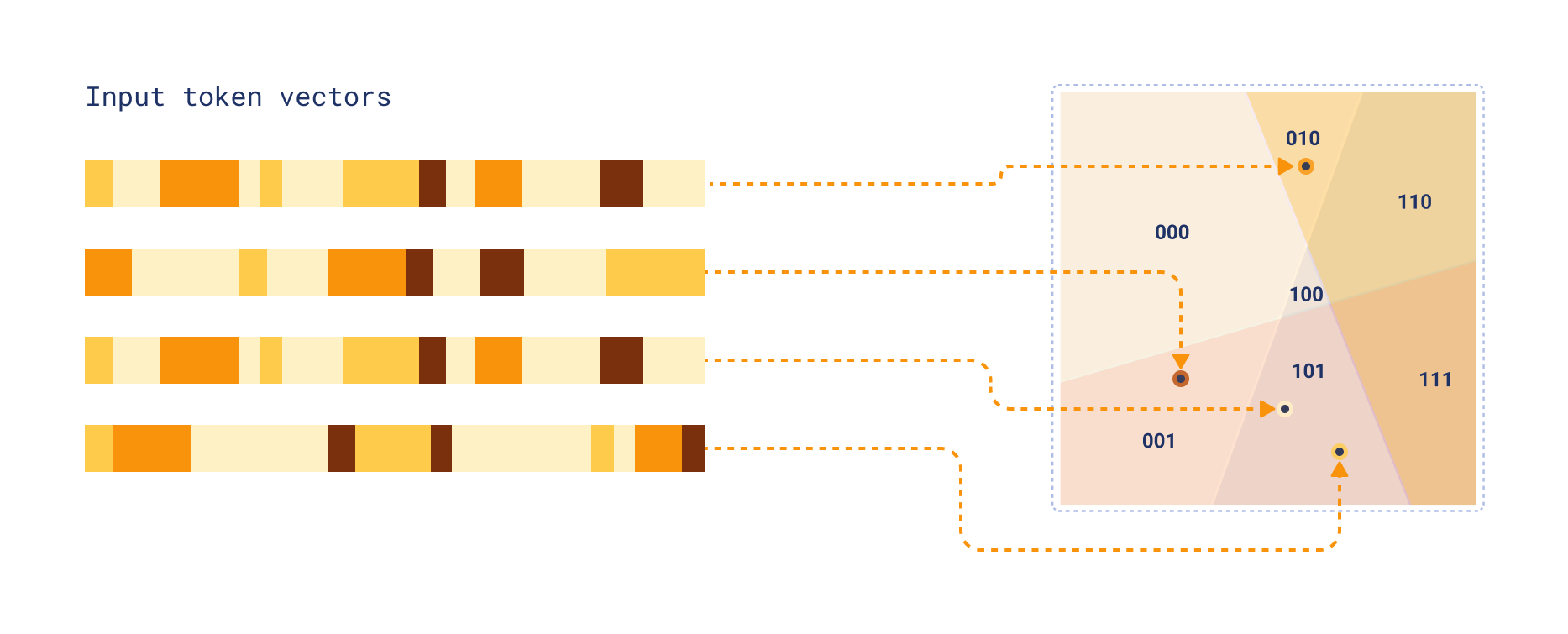
Each token vector is now assigned to one of these regions based on which side of each hyperplane it falls on. This is
done by computing the dot product of the input vector with each hyperplane normal vector, and taking the sign of each
result. Since each of our regions can be represented as a binary string of length k_sim (where each bit indicates
which side of a hyperplane the vector is on), we can interpret this binary string as an integer to get a cluster ID.
Fixed Dimensional Encoding (FDE) creation
Once all input vectors are assigned to clusters, we can aggregate the vectors belonging to each of the clusters. This process is slightly different for documents and queries. In both cases, we’ll end up with a fixed-dimensional vector with the same number of dimensions, but the way we compute these vectors differs.
Document clustering
Once we have assigned all the document token vectors to clusters, we compute the cluster centroids by averaging all vectors in each cluster. This gives us a representative vector for each cluster. If a cluster ends up being empty (i.e., no vectors were assigned to it), we fill it using vector from the nearest non-empty cluster. The distance between clusters is determined by the Hamming distance between their cluster IDs.
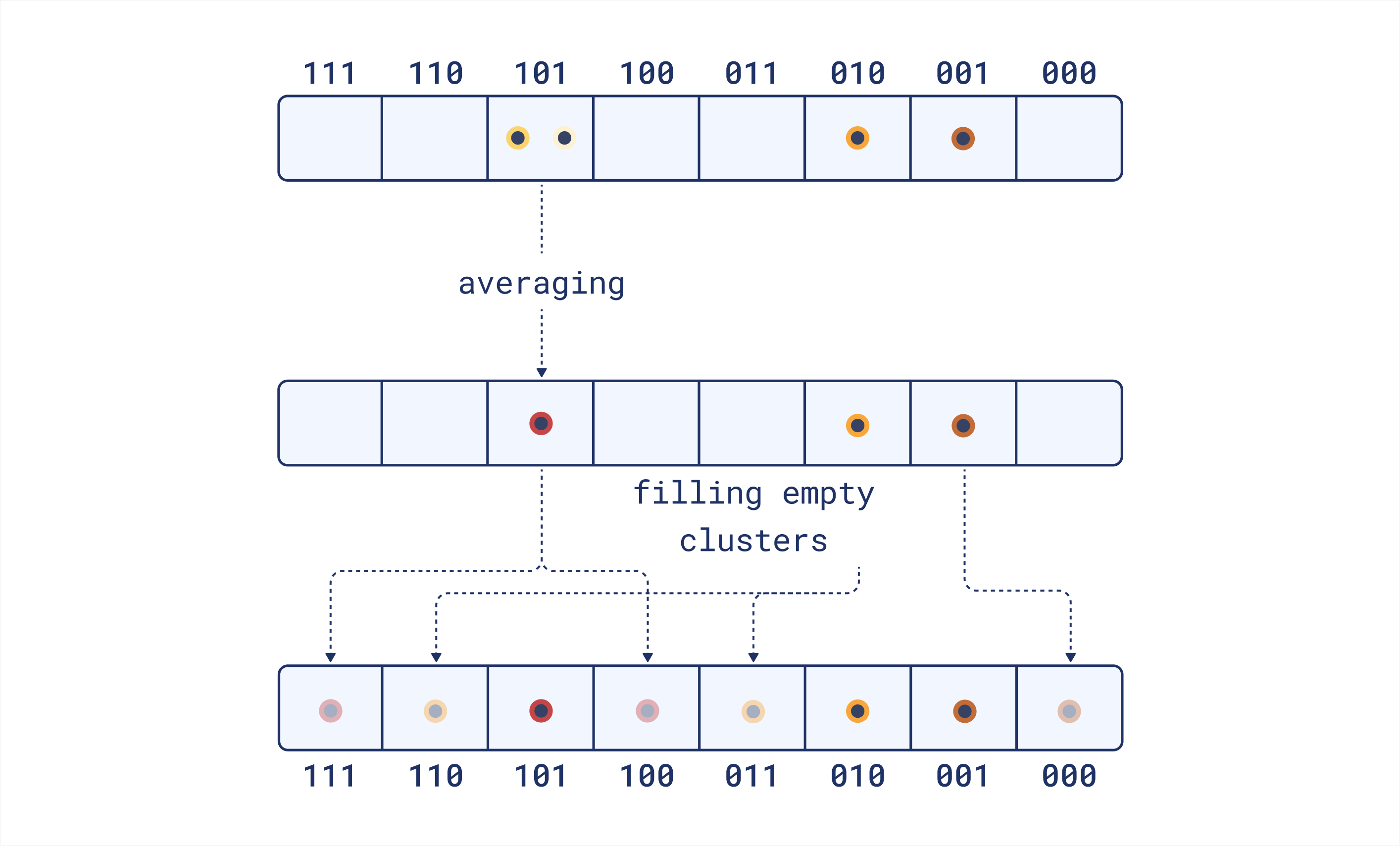
As a result we get 2^k_sim vectors, each of them being dim-dimensional.
Query clustering
Query processing is slightly different. Instead of computing the average vector for each cluster, we compute the sum of all vectors in each cluster. This means that the resulting vectors will have larger magnitudes for clusters with more assigned vectors. The idea is that it preserves the natural distribution of query terms, which can be beneficial for retrieval. Unlike with documents, we do not fill empty clusters for queries. Queries are typically shorter than documents, so it’s more likely that some clusters will be empty. Filling them could introduce noise and distort the representation, as each term would contribute to the dot product multiple times.
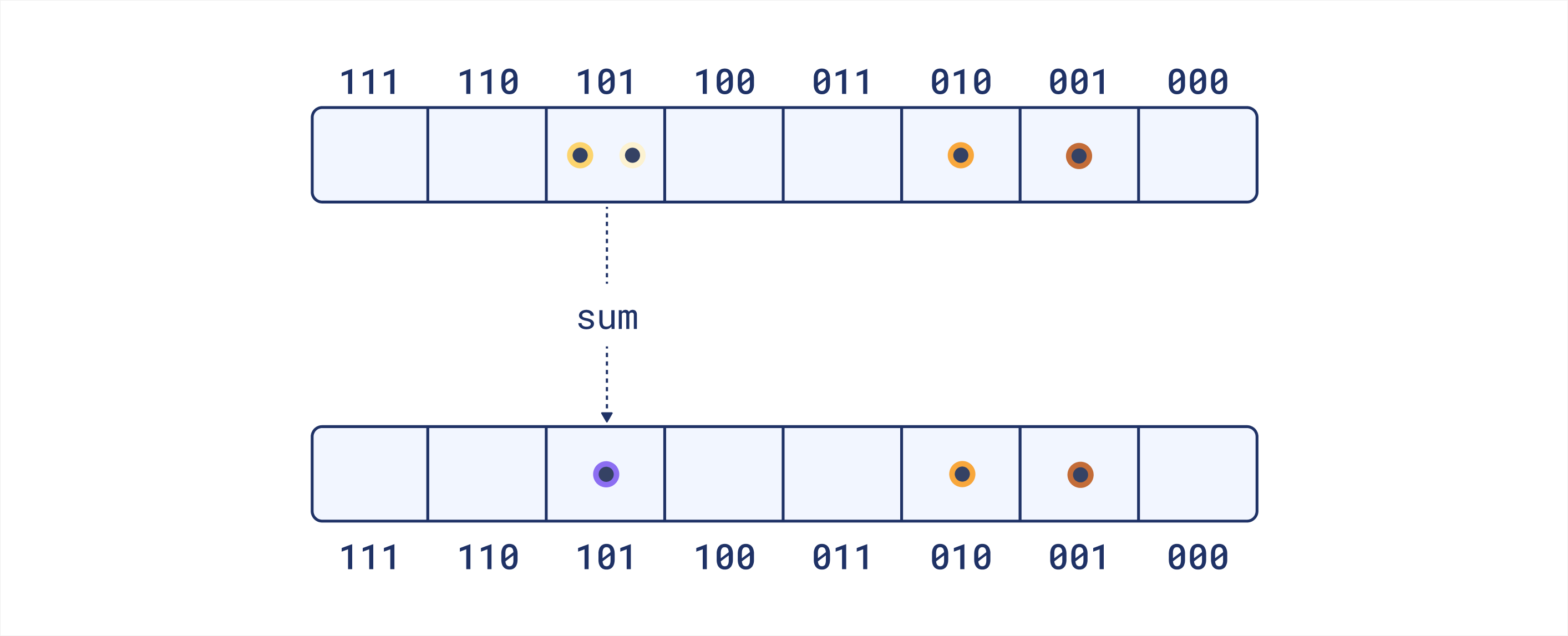
Again, we end up with 2^k_sim vectors of size dim. Because we do not fill empty clusters, some of these vectors
might be zero vectors.
Dimensionality reduction through Random Projection
The paper reports results from experiments with k_sim values of 4 and 5. Practically, this means 16 or 32 clusters,
respectively. If the original token vectors have a dimensionality of 128, the resulting FDE would have a dimensionality
of 16 * 128 = 2048 or 32 * 128 = 4096. However, a single SimHash projection with just 4 or 5 hyperplanes might not
capture enough information about the input vectors. To improve the quality of the FDEs, the authors suggest repeating
the process multiple times with independent SimHash projections and concatenating the results. Practically, with
r_reps=20 repetitions, we would end up with FDEs of size 20 * 16 * 128 = 40960 or 20 * 32 * 128 = 81920, which is
quite large and could slow down single-vector search significantly. For that reason, the authors suggest applying random
projection to reduce the dimensionality of each FDE. This involves multiplying each cluster vector by a random
matrix with entries from {-1, +1} and applying a scaling factor of 1/√(dim_proj). This matrix has a shape of
(dim, dim_proj), where dim_proj is the desired dimensionality of the projected vectors. The resulting FDE will then
have a size of r_reps * 2^k_sim * dim_proj.
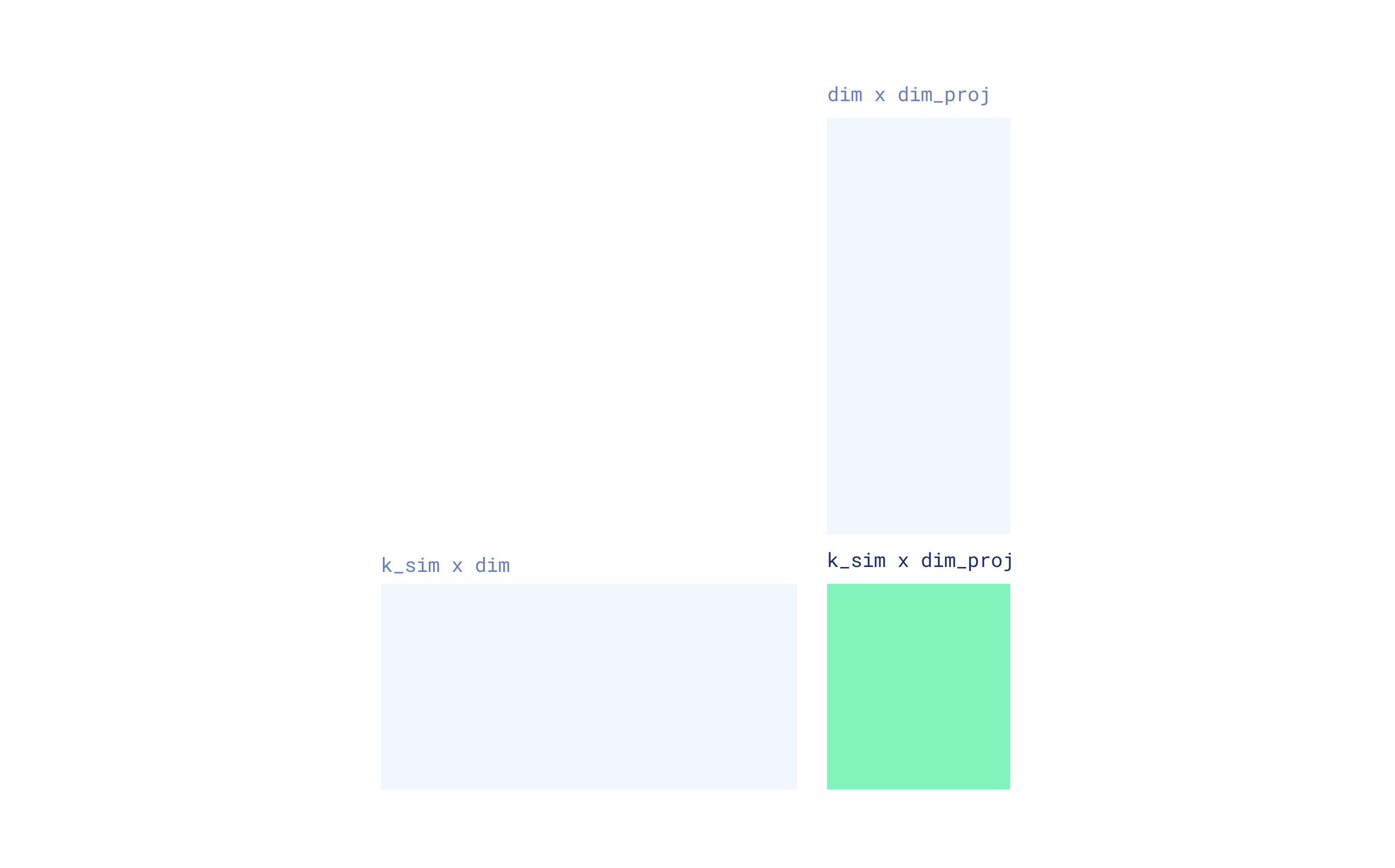
The results from all repetitions are then concatenated to form the final FDE. This repetition helps to create a more robust representation that better approximates the original multi-vector embedding.
Final random projection
The original paper suggests applying an additional random projection to the final FDE to further reduce its
dimensionality. It is an optional step that can be used if the resulting FDE is still too large. This final projection
uses another random matrix with entries from {-1, +1} to project the FDE to a desired lower dimensionality.
Practical considerations
MUVERA embeddings seem to be a promising approach to make multi-vector retrieval more efficient. The paper recommends using it as an initial retrieval step followed by reranking with the original multi-vector representation. This approach requires storing both the MUVERA embeddings and the original multi-vector representations, which increases storage requirements.
Please note that the MUVERA embeddings might be way larger than the single dense vectors produced by traditional
embedding models you might be used to. For example, using k_sim=6 (64 clusters), dim_proj=32, and r_reps=20 with
128-dimensional token vectors results in FDEs of size 20 * 64 * 32 = 40960. This is significantly larger than typical
single-vector embeddings, which are around a few thousand dimensions at most. The increased size of MUVERA embeddings
can impact storage and retrieval efficiency, so it’s important to consider these factors when deciding to use them.
Impact on search performance
To evaluate the effectiveness of MUVERA embeddings, we benchmarked three different approaches on the BeIR nfcorpus
dataset using the ColBERTv2 model. The MUVERA configuration used the following parameters: k_sim=5, dim_proj=16,
and r_reps=20:
| Approach | NDCG@1 | NDCG@5 | NDCG@10 |
|---|---|---|---|
| Full multi-vector (ColBERT) | 0.478 | 0.387 | 0.347 |
| MUVERA-only | 0.319 | 0.267 | 0.242 |
| MUVERA + reranking | 0.475 | 0.383 | 0.343 |
The results show that MUVERA-only search trades some accuracy for speed, achieving about 70% of the full multi-vector performance. However, using MUVERA for initial retrieval followed by multi-vector reranking recovers nearly all the original performance while maintaining the efficiency benefits for the initial search phase.
It’s becoming especially interesting when you consider the search latency improvements. In our benchmarks, we observed significant speed gains:
| Approach | Average Search Time (seconds) |
|---|---|
| Full multi-vector (ColBERT) | 1.27 |
| MUVERA-only | 0.15 |
| MUVERA + reranking | 0.18 |
MUVERA-only search is approximately 8x faster than full multi-vector search, while the hybrid approach with reranking still achieves about 7x speed improvement while maintaining nearly identical search quality.
MUVERA in FastEmbed
FastEmbed provides late interaction text (ColBERT) and multimodal (ColPali) embeddings. Version 0.7.2 has introduced support for MUVERA embeddings which is compatible with any multi-vector representation, and available as a post-processing step.
import numpy as np
from fastembed import LateInteractionTextEmbedding
from fastembed.postprocess import Muvera
# Create a multi-vector model (ColBERT in this case) and then wrap it with MUVERA
model = LateInteractionTextEmbedding(model_name="colbert-ir/colbertv2.0")
muvera = Muvera.from_multivector_model(
model=model,
k_sim=6,
dim_proj=32,
r_reps=20
)
# Create embeddings of the sample text and then process them with MUVERA
embeddings = np.array(list(model.embed(["sample text"])))
fde = muvera.process_document(embeddings[0])
Try it out today
If you’re already using multi-vector retrieval, upgrading to FastEmbed 0.7.2+ will unlock MUVERA’s 7x speed improvements
while maintaining nearly identical search quality. And if you’ve always wanted to experiment with multi-vector retrieval
but were held back by performance concerns or complexity, now is the perfect time to start. MUVERA removes those
traditional barriers, making advanced retrieval techniques accessible and practical for production use. Simply upgrade
your FastEmbed installation with pip install --upgrade fastembed and start benefiting from the power of multi-vector
search without the traditional speed penalties.


