Untangling Relevance Score Boosting and Decay Functions
Evgeniya Sukhodolskaya
·September 01, 2025

On this page:
A problem we’ve noticed while monitoring the Qdrant Discord Community is that due to the extensive list of expressions that the score boosting functionality provides, there’s room for confusion on how it’s supposed to be applied. And that might block you from moving the business logic behind relevance scoring into the Qdrant search engine. We don’t want that!
In this blog, we’d like to de-spooky-fy the decay functions part of the score boosting, or, more precisely: LinDecayExpression, ExpDecayExpression, and GaussDecayExpression – frequent guests on the Discord #ask-for-help channel.
Purpose of Decay Functions
Decay functions help turn numeric properties of your dataset items (like sizes or ratings) into values between 1.0 (most relevant) and 0.0 (not relevant). This makes it possible for those properties to meaningfully influence the final relevance score.
Decay functions are useful when a change in some numeric property of an item should smoothly and proportionally affect its relevance score.
Think of it like this:
- News articles become less relevant over time, so relevance decays with days passed from the publication date.
- A further restaurant is less relevant for food ordering, so relevance decays as the distance to the user increases.
- A better reputation makes a movie more relevant, so relevance decays as the number of positive IMDb reviews decreases.
Three Options
Qdrant has added three decay functions to the score boosting functionality, each one capturing a different way in which relevance can decay.
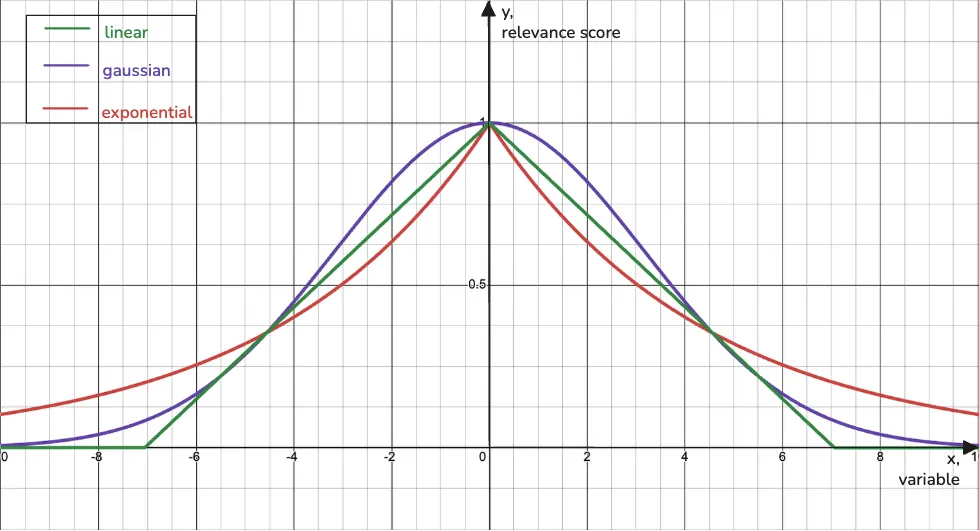
Image 1. Three decay functions used in the score boosting.
An interactive version of this graph is available here.
Linear
Relevance changes at a constant rate with the variable. Each change in the value has the same impact.
→ For example, the discount percentage: the more, the merrier!
Gaussian
Relevance decays smoothly and gradually. Small deviations from the ideal are forgivable, but the further you go, the less relevant it becomes.
→ Perfect for things like product price; small differences are usually fine for users, but when the price gap gets big, interest drops off fast.
Exponential
Relevance drops sharply with even small changes. Deviation from the ideal is punished quickly.
→ Delivery time is a great candidate here. If the item takes too long to arrive, users instantly lose interest.
All three decay functions in Qdrant are symmetrical. They assign 1.0 relevance to a certain value of a variable and decay toward 0.0 as the variable deviates from this target.
This symmetry is useful when there’s a clear “ideal” value, and anything more or less than that is equally off. For example:
- A user has a target price in mind. Anything more expensive is less relevant (obviously), but anything cheaper might also raise quality concerns. (Yes, not always, but many think so.)
- You’re searching for a 30-minute exercise video. Both 25 and 35 minutes are okay-ish, but 5 minutes or 1 hour are clearly not what you had in mind.
Decay Function Parameters
To use decay functions for score boosting, you need to figure out what values to provide for their parameters.
At first glance, it might seem like there are many of them: x, target, midpoint, scale…
Let’s demystify these. And let’s start with a quick win: two of them, x and target, we’ve already used many times in the examples above.
x parameter
This is just the variable you want to transform with a decay function: score, time, distance, age, number of reviews, price, etc.
You can think of it as the input value. It may come from a payload field of an item or the embedding similarity score. Basically, it’s the x-axis of the decay function (and y is the output, the relevance score, decaying from 1.0 to 0.0).
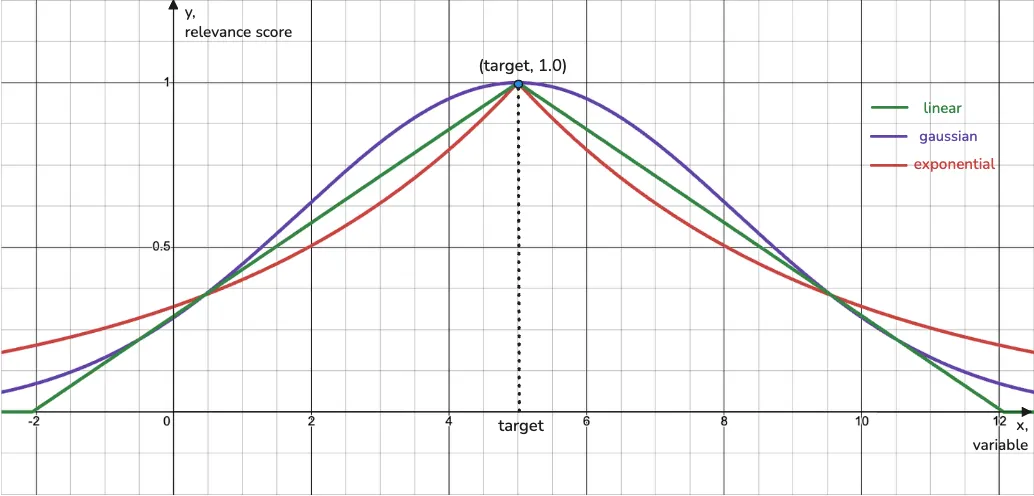
Image 2. x (x-axis) and target (point on x-axis) of a decay function.
An interactive version of this graph is available here.
target parameter
This is the value your x variable needs to match for the item to be considered 100% relevant, to get a 1.0 relevance score from the decay function.
By default, target is 0.0, which makes sense in many scenarios. For example:
- 0.0 meters for delivery distance: the closer, the better.
- 0.0 seconds since publishing: the fresher, the better.
But of course, target can be anything else, depending on your use case: desired and most relevant price, age, size, score, etc.
So, in short, x is the current value, target is the relevance best-case value.
scale & midpoint parameters
Now we’re left with midpoint and scale. What’s their purpose? To control how the decay function of your choice will, well… function. Its shape needs to match your definition of relevance and the nature of the variable you’re transforming.
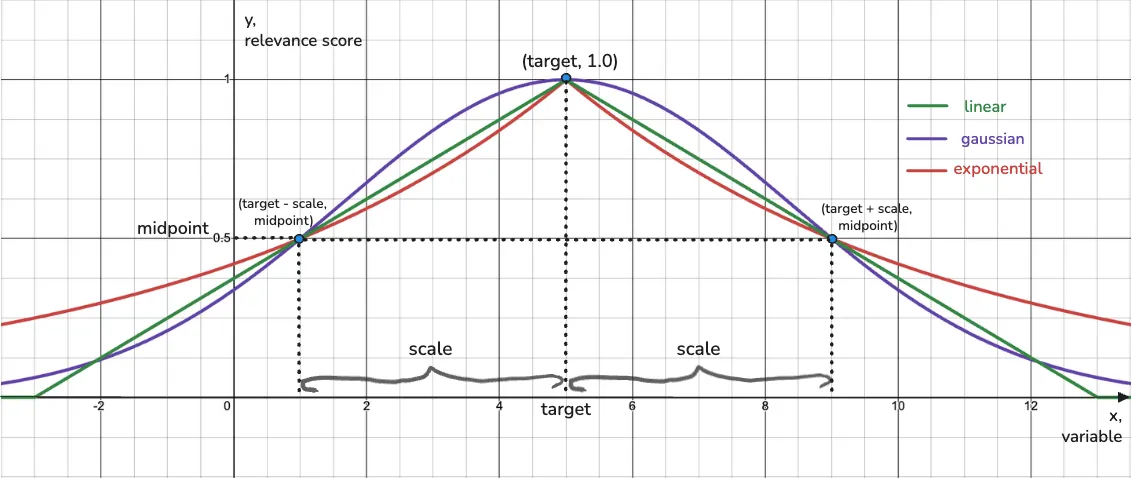
Image 3. scale (segment on x-axis) and midpoint (point on y-axis), defining the shape of decay functions.
An interactive version of this graph is available here.
Together, scale and midpoint define the slope of the function, how quickly or smoothly relevance decays. It reads: “To what scale should x change to reach a midpoint value of relevance.”
A decay function’s shape is defined by two key points:
- (
target, 1.0) — the ideal use case - (
target ± scale,midpoint) — how relevance drops after thexvariable changes byscalefrom the idealtargetvalue.
The choice of scale and midpoint defines a certain behavior for each type of decay function.
- For Gaussian decay, relevance drops slowly and smoothly from 1.0 toward
midpoint, asxchanges byscale. After that, the decay accelerates. - For Exponential decay, it’s the opposite: fast decay at first till
midpoint, then slower. - For Linear decay,
midpointandscaledefine the point at which the relevance score hits 0.0, as it’s the only decay function that actually reaches zero.
Note #1. midpoint defaults to 0.5, but can be anything in the (0.0, 1.0) range. For linear decay, it’s also valid to set midpoint to 0.0.
Note #2. scale defaults to 1.0, but it can be anything that reflects the relationship between your variable x and how you define relevance. Only you know what makes sense here.
Note #3. We expect scale to be a positive value; it just makes calculations for us simpler.
Note #4. Exponential and Gaussian decay functions never reach 0.0. The relevance score approaches zero but stays positive. Only Linear decay can reach exactly 0.0, and it’s the only one where setting midpoint to 0.0 is valid.
How to Pick Parameters: Examples
Example #1
Use case: A user is searching for educational videos in German about techno club culture to practice language comprehension. They’ve chosen 5 minutes as the ideal video length.
Decay: Gaussianx: Video length in minutes, stored in the video’s payloadtarget: 5 (minutes)scale: 4 (minutes)midpoint: 0.5
Explanation:
We assume that, out of all videos relevant by content, the user will tolerate deviations in video length by up to ±4 minutes, so 1-minute to 9-minute videos. Relevance should therefore decay smoothly and slowly from 1.0 to 0.5 in a Gaussian fashion.
Anything longer than 9 minutes or shorter than 1 minute quickly becomes less relevant, even if the content still matches.
Example #2
Use case: A promo code aggregator app boosts freshness to always show the latest promo codes for products and events.
Decay: Exponentialx: datetime of promo code upload, stored in the payloadtarget: Current datetime (moment of search)scale: 604800 (1 week in seconds)midpoint: 0.1
Explanation:
Out of all promo codes for different products/events, users will strongly prefer ones uploaded just now, as they’re most likely to work. But that relevance drops quickly over time: within a week, it reaches a midpoint of 0.1. After that, if a promo code is still active, it’s a gamble anyway: might work, might not. So old-but-not-expired codes are roughly equally irrelevant.
Note #5. For Qdrant datetime payloads, scale should always be provided in seconds!
I Don’t Know All the Parameters in Advance
As you can see, using decay functions in Qdrant’s score boosting means you’ll have to know the parameters in advance.
What we’ve seen in our Discord Community quite a few times is that people try to apply decay functions to normalize similarity scores from prefetches, usually as a way to fuse results from different types of similarity searches.
The common question is:
How can I use a decay function for score normalization if I don’t know the scale in advance?
The answer is: you can’t dynamically set the midpoint and scale parameters, hence you can’t dynamically normalize scores, and you probably shouldn’t even try:
Say you’re prefetching a subset of items scored by a late interaction model like ColBERT, where a higher score means higher similarity. You get scores like 36, 22, and 1. Separately, you also have cosine similarity scores from some dense vector search, and you’d like to fuse both sets of results.
If you normalize ColBERT scores dynamically, based on just this subset, 36 will become 1.0, and everything else scales accordingly.
But here’s the problem: That 36 might not be a “high” score at all. Maybe your dataset just didn’t contain any good matches. The normalization step will strip away that context, and when you fuse the scores, you’ll create a false sense of high relevance.
If you’re planning to use a decay function for score normalization, you need to know the expected parameter values beforehand. If you don’t know the range of your input variable (x), you won’t be able to use a decay function reliably.
Code Snippets
Now let’s see how using decay functions looks in Qdrant.
We’ll provide HTTP request examples, but you can use decay functions analogously in the Python, TypeScript, Rust, Java, C#, and Go clients.
Note #6. Payload variables used within the formula benefit from having payload indexes. So, we require you to set up a payload index for any variable used in a formula.
Let’s take our “educational videos in the German language” example and see how it takes shape in Qdrant:
POST collections/video/points/query
{
"prefetch": {
"query": <video_description_embedding>,
"limit": 10 // limit of prefetched results
},
"query": {
"formula": {
"sum": [
"$score", // so the final score = score + gauss_decay(duration)
{
"gauss_decay": {
"target": 5,
"scale": 4,
"midpoint": 0.5,
"x": "duration" // payload key
}
}
]
}
}
}
And here’s the “fresh promo codes” example, so you’ve got a better grip on how to use Qdrant’s score boosting:
POST collections/promocodes/points/query
{
"prefetch": {
"query": <promocode_description_embedding>,
"limit": 10 // limit of prefetched results
},
"query": {
"formula": {
"sum": [
"$score", // so the final score = score + exp_decay(search_time - upload_time)
{
"exp_decay": {
"x": {
"datetime_key": "upload_time" // payload key
},
"target": {
"datetime": "2025-08-04T00:00:00Z" // time of the search
},
"scale": 604800, // 1 week in seconds
"midpoint": 0.1
}
}
]
}
}
}
Note #7.datetime_key and datetime are used to distinguish between payload keys that hold a datetime-type string and directly provided datetime strings.
To Sum Up
So, we’ve covered quite a bit, including:
- What decay functions are and why they matter;
- How
target,x,scale, andmidpointshape decay behavior; - And how to use decay functions in Qdrant’s score boosting.
We truly hope this write-up helped untangle things a bit. Now the only thing left for you is to get your hands dirty and experiment!
Use the snippets in the article as a starting point and experiment with the relevance score boosting in Qdrant Cloud. We offer a free-forever 1GB cluster: enough to test, tweak, and see how the decay functions behave on your data.
And if you feel like diving deeper into decay functions or score boosting in general, check out our documentation, which includes a decay-on-distance example and plenty more to learn from.
Tell Us What You’re Building
We’d love to hear what you’re experimenting with! What are you considering “relevant”? Which features of the last releases are you enjoying? What’s missing?
If you’re still unsure about anything, feel free to ask us on Discord or connect with me on LinkedIn. We’re always happy to explain more, and we’d love to know what to write about next!


































