Qdrant Overview
Welcome!
Whether you’re getting started with Qdrant Open-Source or Cloud, this brief primer will help you with understanding an overview of the platform. It’s highly recommended you read this overview before starting your development with Qdrant!
Retrieval Process
Vector search is a transformative information retrieval technique that goes beyond keyword matching to find data based on semantic meaning. It begins with embedding models, which convert unstructured data (text, images, audio) into dense vector embeddings, fixed-length lists of numbers that represent the data’s conceptual essence. These vectors are mapped into a high-dimensional vector space, where items with similar meanings are positioned closely together. This spatial organization allows a search for “climate change” to retrieve documents about “global warming,” even if the exact words differ.
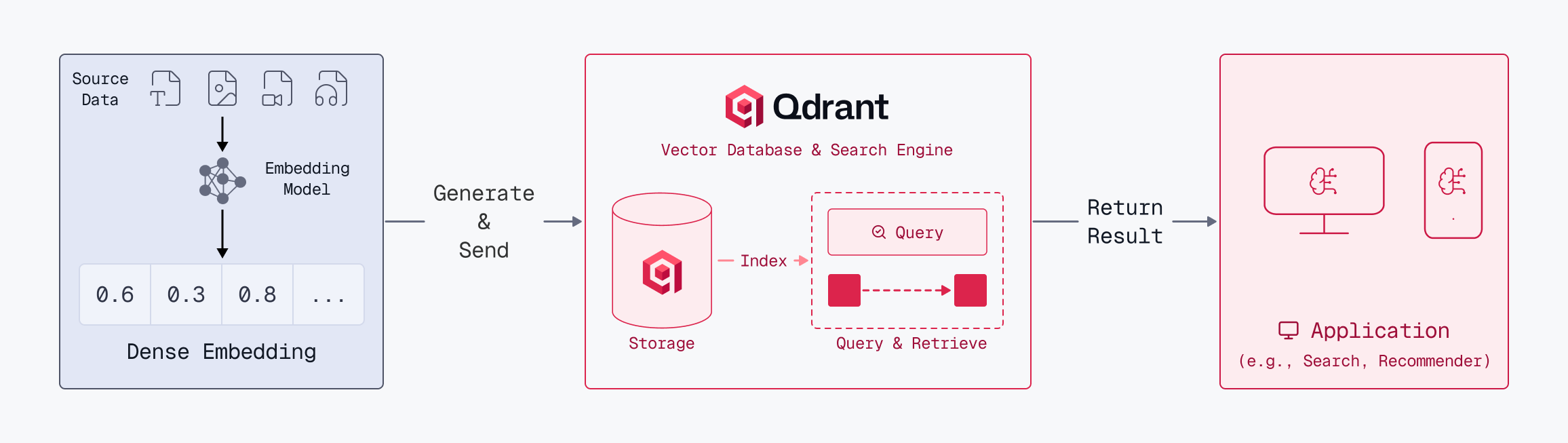
While dense vectors excel at capturing context, they can sometimes miss specific technical terms or unique identifiers. To bridge this gap, Qdrant also utilizes sparse vectors designed to capture precise lexical matches for specific keywords. Learn more in this guide.
The process of generating embeddings from unstructured data is called inference. On Qdrant Cloud, you can use Cloud Inference to let Qdrant generate embeddings on the server side. Alternatively, you can use a library like FastEmbed to generate embeddings on the client side.
The search process itself revolves into the concept of Top-K retrieval. When a user submits a request, it is instantly transformed into a query vector. The engine then calculates the similarity between this query vector and document vectors, returning the “Top-K” closest matches, where K is a user-defined number representing the desired volume of results. This allows developers to fine-tune the balance between the breadth of the search and the precision of the answers.
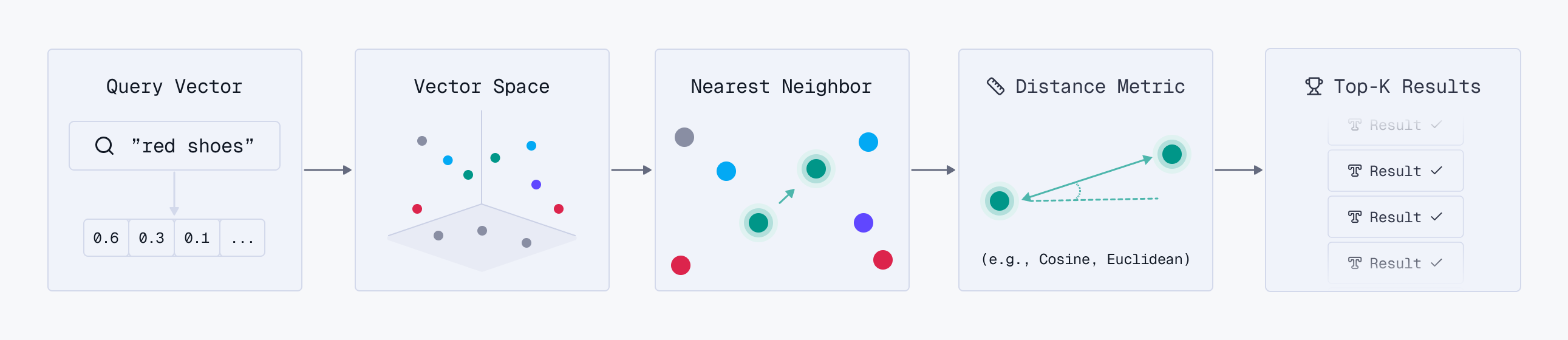
To deliver the most robust search experience, Qdrant enables Hybrid Retrieval with semantic and lexical search, which you can learn more about here.
Architecture
Qdrants operates in a client-server architecture, providing official client libraries for Python, JavaScript/TypeScript, Rust, Go, .NET, and Java. However, Qdrant exposes HTTP and gRPC interfaces to facilitate integration with virtually any programming language.
Data Structure
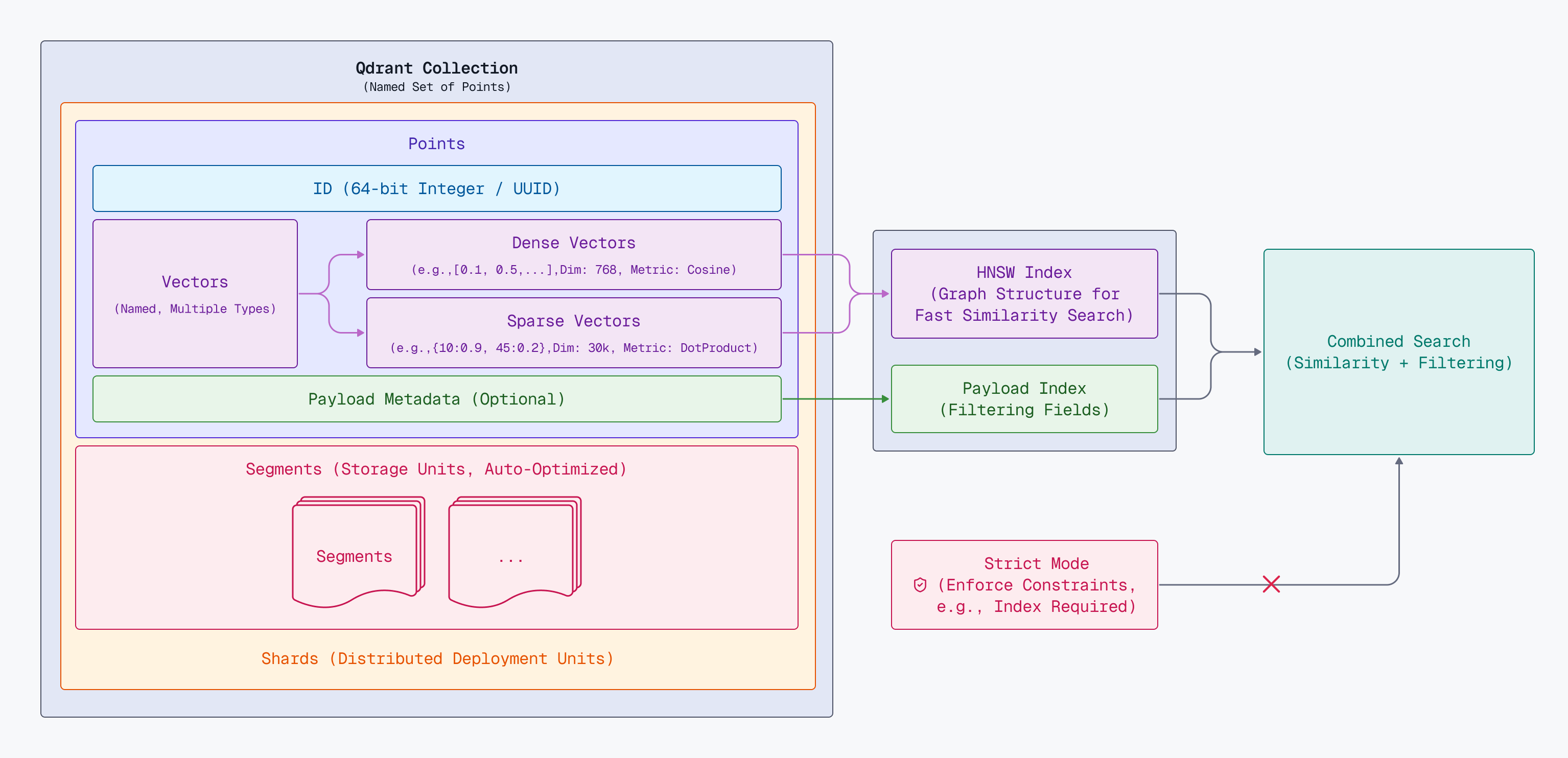
Qdrant collections are designed for horizontal and vertical scaling. You can learn about the details in the above diagram from links below:
Deployments
Qdrant supports multiple deployment models to match different infrastructure and operational needs. The right option depends on your security constraints and operational model: Qdrant-managed infrastructure (Managed Cloud), shared responsibility with your own clusters (Hybrid Cloud), or full ownership and independence (Private Cloud or Open Source).
| Feature | Benefits | OSS | Managed | Hybrid | Private |
|---|---|---|---|---|---|
| Deployment | Choose how and where to deploy your Qdrant vector database based on your infrastructure needs. | ✅ | ✅ | ✅ | ✅ |
| High Availability | Automatic failover and replication to ensure your vector search is always available. | ❌ | ✅ | ✅ | ✅ |
| Zero-Downtime Upgrades | Upgrade your Qdrant database without any service interruption using replication. | ❌ | ✅ | ✅ | ✅ |
| Monitoring & Alerting | Built-in monitoring and alerting to observe the health and performance of your clusters. | ❌ | ✅ | ✅ | ❌ |
| Central Management UI | A unified console to create, configure, and manage all your Qdrant database clusters. | ❌ | ✅ | ✅ | ❌ |
| Horizontal & Vertical Scaling | Scale your clusters up, down, or out with automatic shard rebalancing and resharding support. | ❌ | ✅ | ✅ | ✅ |
| Backups & Disaster Recovery | Automated backups and restore functionality to ensure data durability and graceful recovery. | ❌ | ✅ | ✅ | ✅ |
| Data Privacy & Control | Keep all user data within your own infrastructure and network, not accessible by external parties. | ✅ | ❌ | ✅ | ✅ |
| Multi-Cloud & On-Premises | Deploy on AWS, GCP, Azure, on-premises, or edge locations based on your requirements. | ✅ | ❌ | ✅ | ✅ |
| Enterprise Support | Access to Qdrant’s enterprise support services for production deployments. | ❌ | ✅ | ✅ | ✅ |
| No Infrastructure Management | Qdrant fully manages your infrastructure, so you can focus on building your application. | ❌ | ✅ | ❌ | ❌ |
Scaling Considerations
The default configuration of Qdrant is sensible when you are starting to work on a POC or your side project. However, when transitioning to production and experiencing the growth of data size and concurrent users, your expectations regarding high availability, latency, or throughput will change. If you foresee scaling the service, you should build your system ready for these kinds of challenges from the outset. There are a few common scenarios you should be aware of, especially if you are taking your first steps with Qdrant, anticipate rapid growth soon, and want to make your system future-proof.
Memory Requirements
Memory is a critical resource when scaling vector search. By default, Qdrant stores vectors in RAM for maximum search performance, but as collections grow to millions of vectors, keeping everything in memory becomes expensive. Qdrant lets you control the memory usage by offloading data to disk, and you can enable that mechanism at any time, even on an existing collection:
- Frequently accessed vectors naturally stay cached, while others are read from disk only when needed, if you store vectors on disk
- Graph traversal may require IO operations if you store the HNSW index on disk
Put both on disk only when RAM is severely constrained, and ensure you have fast NVMe storage.
Filtering
Vector search alone can provide a decent search experience to your users; however, semantic similarity is rarely the only factor you have to consider. Embeddings won’t capture attributes such as price, and typically, a filter on a specific payload attribute has to be applied. To make that filtering effective, there are some specific Qdrant mechanisms you should be aware of, including with payload indexes.
Payload Indexes
The payload index is a helper data structure that enables effective filtering on a particular payload attribute. It’s a concept familiar from relational databases, where we create an index on a column that we often filter by. Similarly, in Qdrant, you should also make a payload index on a field used for filtering.
A unique aspect of the payload index is that it extends the HNSW graph, allowing filtering criteria to be applied during the semantic search phase. That means it’s a single-pass graph traversal, rather than pre- or post-filtering, which both have some drawbacks.
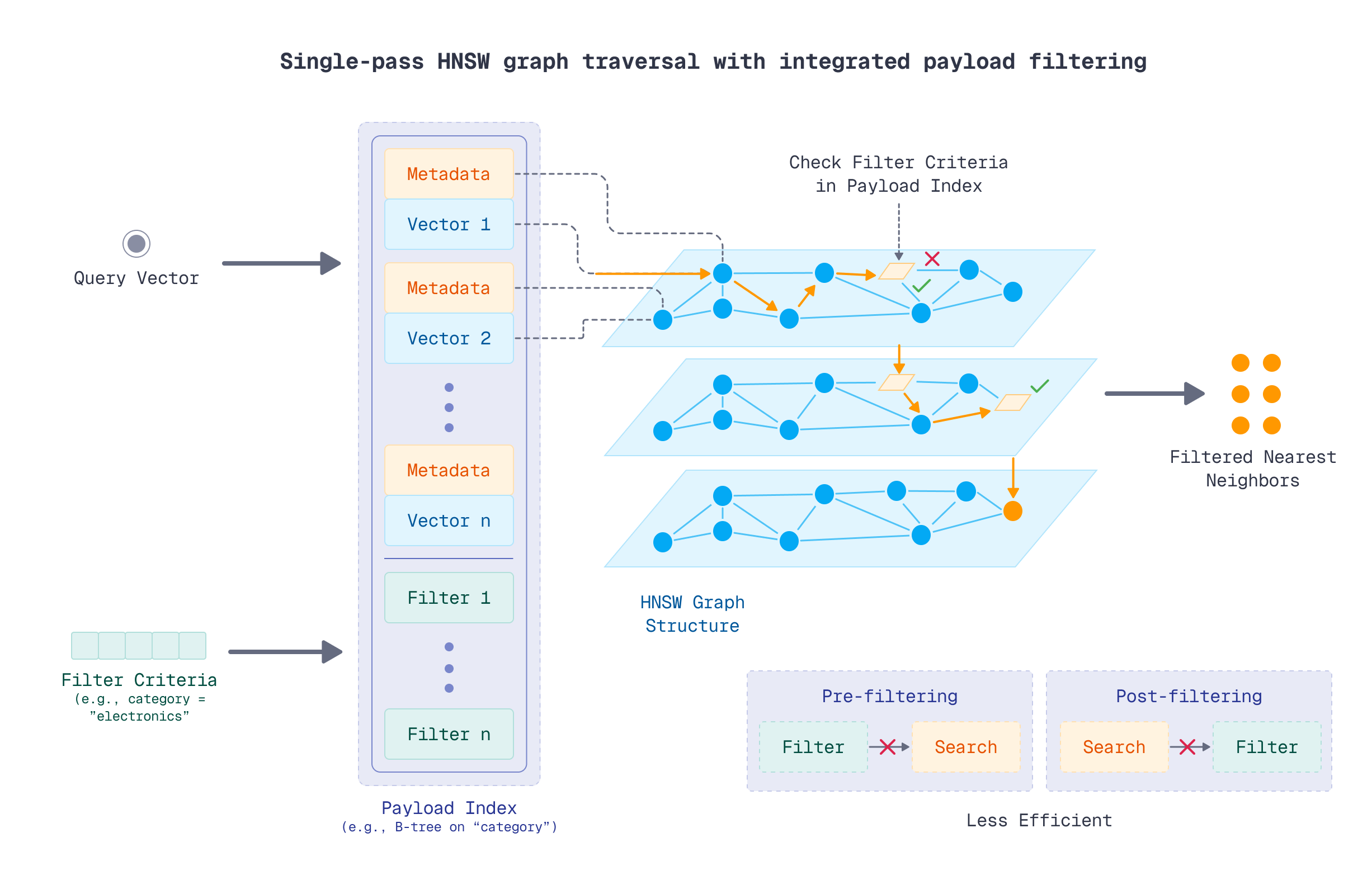
The fact that a payload index extends the HNSW graph means it’s more efficient to create it before indexing the data, as the optimizer will need to build the graph once. However, in some cases, you may already have a collection with a lot of vectors and recognize a need to filter by a specific attribute. In such cases, you can still create a payload index, yet it won’t immediately affect the HNSW graph.
ACORN is an additional mechanism that can improve the search accuracy if you have multiple high cardinality filters in your search operations.
Scaling
Vertical scaling has natural limits - eventually, you’ll hit the maximum capacity of available hardware, and single-node deployments lack redundancy. Optimize scaling with sharding, replication, and segment configuration options.
Sharding
Qdrant uses sharding to split collections across multiple nodes, where each shard is an independent store of points. A common recommendation is to start with 12 shards, which provides flexibility to scale from 1 node up to 2, 3, 6, or 12 nodes without resharding. However, this approach can limit throughput on small clusters since each node manages multiple shards.
For optimal throughput, set shard_number equal to your node count (read more here). If you want to have better control over sharding, Qdrant supports custom shards.
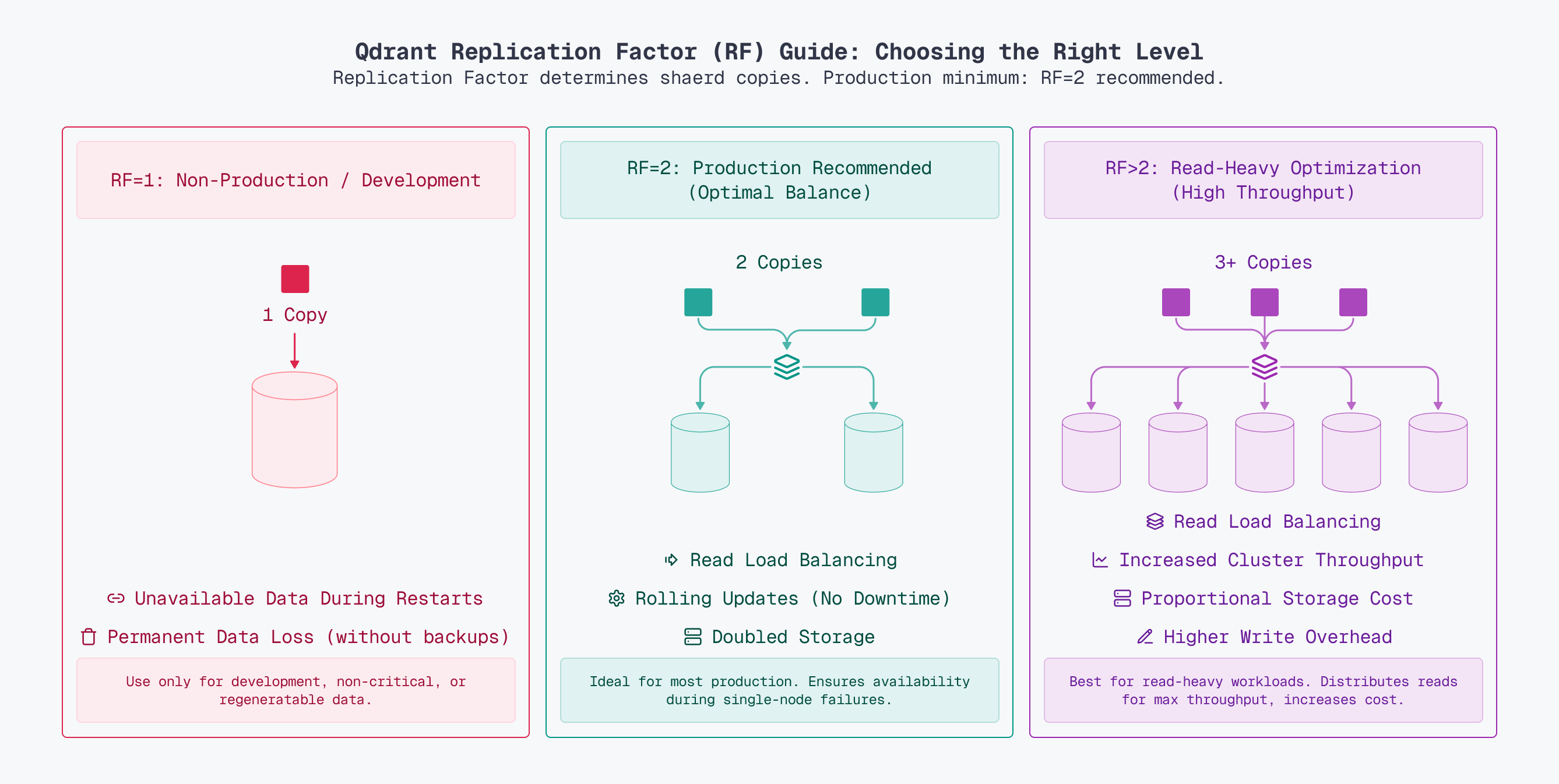
Replication
The replication factor determines how many copies of each shard exist. For production systems, a replication factor of at least 2 is strongly recommended.
Segment Configuration
Each shard stores data in multiple segments. A segment stores all the data structures of a subset of the points in a shard. Fewer segments create larger segments with better search throughput, as larger HNSW indexes require fewer comparisons. However, larger segments take longer to build and recreate, slowing writes and optimization. More segments mean faster indexing but lower search performance since queries scan more segments. Read more on segment configuration.
Safety
Some of the collection-level operations may degrade performance of the Qdrant cluster. Qdrant’s strict mode prevents inefficient usage patterns through multiple controls: it may block filtering and updates on non-indexed payload fields, limit query result sizes and timeout durations, restrict the complexity and number of filter conditions, cap payload index counts, constrain batch upsert sizes, enforce maximum collection storage limits (for vectors, payloads, and point counts), and implement rate limiting for read and write operations to prevent system overload.
The OSS version does not enforce anything, but please consider enabling and configuring strict mode settings according to the application needs. Otherwise, some of the API calls may impact the performance of your cluster by using Qdrant in a suboptimal way.
Getting Help
If you’re new to Qdrant, start with the free Essentials Course, which covers core concepts and best practices. For questions, troubleshooting, and community support, join the Discord Community - it’s the best place to get help from both Qdrant users and the core team. Paid customers have access to the Support Portal through the Qdrant Cloud Console, for direct technical assistance and priority response times.


